Statistisches Lernen und das Erkennen mathematischer Strukturen

Im ersten Blogartikel habe ich beschrieben, dass Mathematik in besonderer Weise die begrenzten Ressourcen für unser System 2 erfordert, und im letzten Artikel die Frage gestellt, wie es trotz der begrenzten Ressourcen zu der heutigen komplexen Mathematik kommen konnte. Einen ersten Ansatz dazu habe ich im letzten Artikel ebenfalls beschrieben, nämlich, dass sich mathematische Sachverhalte durch unterschiedliche Darstellungen erfassen lassen, die teilweise einen besseren Zugang für System 1 erlauben (bildliche Darstellungen). In diesem Artikel möchte ich eine weitere Operation von System 1 vorstellen, die zur Entwicklung und zum Lernen von Mathematik beiträgt. Sie ermöglicht uns das Erkennen mathematischer Strukturen.

Lernen als statistischer Prozess

Betrachten Sie das folgende Bild:

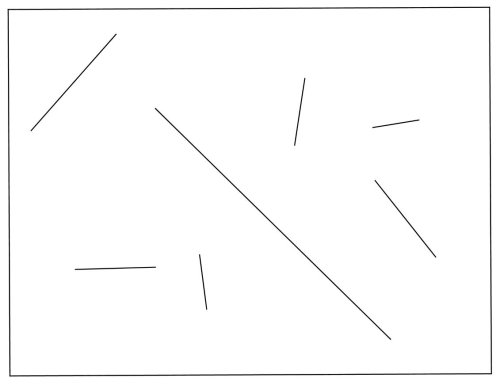
Nach Daniel Kahneman zeigen Studien, dass Probanden durchaus gute Schätzungen abgeben, wenn man sie auffordert, eine Strecke mit der durchschnittlichen Länge der abgebildeten Strecken zu zeichnen. Das gilt hingegen nicht, wenn man sie auffordert, eine Strecke mit der Gesamtlänge der abgebildeten Strecken zu zeichnen. Kahneman nutzt diesen Befund mit einem ähnlichen Bild in seinem Buch „Schnelles Denken, langsames Denken“ als einfaches Demonstrationsbeispiel dafür, wie Menschen Mengen repräsentieren, nämlich durch einen Durchschnittswert mit einer gewissen Varianz. Das führt dazu, dass die durchschnittliche Streckenlänge durchaus gut abgeschätzt werden kann, aber die summarische Streckenlänge nicht (vgl. Kahneman 2015, S.121f).

Stellen Sie sich dazu noch folgende Situation vor: „Die große Maus kletterte über den Rüssel des sehr kleinen Elefanten.“ Sie werden sich vorstellen, wie eine Maus, die nicht größer ist als ein Schuhkarton, über den Rüssel eines Elefanten klettert, der größer als ein Sofa ist (auch dieses Beispiel stammt von Kahneman 2015, S. 100). „Maus“ und „Elefant“ sind Kategorien oder Namen für eine Menge von Tieren und sie haben eine Vorstellung davon, wie eine Maus oder ein Elefant normalerweise aussieht. Und normal meint, wie diese Tiere im Durchschnitt aussehen, wobei eine gewisse Varianz erlaubt ist. Das macht es unwahrscheinlich, dass die Maus in ihrer Vorstellung größer als der Elefant oder auch nur etwa genau so groß wie der Elefant gewesen ist.

So einen durchschnittlichen Elefanten, für den eine gewisse Varianz erlaubt ist, nennen wir einen Prototyp für einen Elefanten. Ein anderes mögliches Wort dafür ist die Norm eines Elefanten, weil dadurch festgelegt wird, was für einen Elefanten normal ist. Die Bildung eines solchen Prototypen oder einer Norm geschieht automatisch, größtenteils unbewusst und mühelos – sie ist eine Operation von System 1. Und sie bildet in vielen Bereichen das ab, was wir als „Lernen“ bezeichnen. Wenn wir das erste Mal einen Elefanten sehen, dann besteht die gesamte Kategorie (oder Menge) „Elefant“ aus diesem ersten Individuum und wenn wir in dieser Situation von „Elefant“ reden, dann meinen wir genau dieses Individuum mit all seinen Eigenheiten. Doch wir lernen schnell von unseren Mitmenschen, dass es noch andere Tiere gibt, die fast genauso aussehen und auch als Elefant bezeichnet werden. „Elefant“ wird vom Namen eines Individuums zum Namen einer Menge von Tieren und diese ist dadurch repräsentiert, dass alle grau, ziemlich groß und schwer sind, dass sie einen Rüssel haben usw. Diese Eigenschaften gehören zum Durchschnitt der Elefanten, die Ihnen begegnet sind, und sie ergeben zusammen einen Prototyp eines Elefanten. Andere Eigenschaften wie Narben oder Hautmusterungen werden Sie nur bei einzelnen Tieren gefunden haben, weshalb diese nicht zum Durchschnitt gehören. So haben wir anhand unserer Beobachtungen gelernt, was die Kategorie „Elefant“ ausmacht, indem wir immer weiter von den Eigenheiten einzelner Tiere absahen. Wir nahmen nur noch das als Eigenschaften der Menge an, was für alle Elefanten ungefähr galt, indem wir die Menge der Elefanten, die wir gesehen haben, durch einen prototypischen Durchschnittselefanten mit einer gewissen Varianz repräsentierten.

Die Varianz für die verschiedenen Merkmale Ihres Prototyps ist jedoch unterschiedlich groß. Bei den Eigenschaften, die sich kontinuierlich anpassen lassen, so wie Größe, Gewicht und Farbton, enthält Ihr Prototyp keine präzise Größe, denn hier kann die Varianz recht groß werden. Andere Merkmale wie der Besitz eines Rüssels sind hingegen notwendige Bedingungen; bei diesen gibt es keine Varianz. So sind wir teilweise zu „harten“ Kriterien gelangt (Besitz eines Rüssels – ohne Varianz) und teilweise zu „weichen“ Kriterien (ungefähre Größe, …).

Mit der Zeit werden Sie einen ziemlichen guten Prototyp gebildet haben, zu dem auch Elefanten passen, die Sie noch nie vorher gesehen haben, denn sie liegen innerhalb der von Ihnen erlernten Varianz. Sie haben in dieser Beziehung scheinbar „ausgelernt“ und das legt den zweiten Begriff der „Norm“ vielleicht eher nahe als er Ihnen oben erschienen ist. Zu diesem Zeitpunkt kann Ihnen niemand mehr eine Maus als Elefanten verkaufen. Wenn Ihnen dieser Satz zu absurd vorkommt, dann denken Sie daran, dass Sie sowohl Maus als auch Elefant als Säugetier kennen, dass es also durchaus eine gemeinsame Kategorie für Maus und Elefant gibt.

Nehmen wir nun an, dass Sie bisher nur afrikanische Elefanten gesehen haben und nun zum ersten Mal auf einen indischen Elefanten treffen. Dies wird Sie überraschen: Ein Tier, das in vielen Bereichen gut zu Ihrer Norm passt und dennoch systematisch davon abweicht. Überraschungen beruhen auf Erwartungen, die verletzt werden. Erwartungen können sehr stark und daher bewusst sein, weswegen man von expliziten Erwartungen spricht. Das wäre im obigen Beispiel vielleicht der Fall gewesen, wenn Sie den indischen Elefanten in einem Zoo gesehen hätten und sie vorher auf der Karte gesehen haben, dass dort das Elefantengehege ist, sodass sie explizit die Ihnen bekannten afrikanischen Elefanten zu sehen erwartet haben.

Häufiger sind implizite, unbewusste Erwartungen, die Ihnen erst bewusst werden, wenn sie verletzt werden, zum Beispiel wenn ein Wort nicht trinkt. Sie hatten beim letzten Satzende keine explizite Erwartung, welches Wort nach „nicht“ kommen würde, aber das Wort „trinkt“ gehörte sicher nicht zu den Wörtern, die sich im Kontext des Satzes erwarten ließen. Solche Überraschungen werden nach Kahneman innerhalb von zwei Zehntelsekunden erkannt, wie neuropsychologische Studien gezeigt haben (vgl. Kahneman 2015, S. 99).

Eine Erwartung lässt sich als Vorhersage verstehen, die auf Ihrem bisherigen Wissen beruht, und eine Überraschung ist dann ein Vorhersagefehler, der etwas Unpassendes in Ihrem bisherigen Wissen aufdeckt. Insofern sind Überraschungen Initiatoren für einen Lernprozess, bei dem Normen angepasst werden. Im obigen Beispiel werden Sie nun die Kategorie „Elefant“ erweitern und evtl. gleich zusätzlich die Untergruppen „Afrikanischer Elefant“ und „Indischer Elefant“ bilden, um die systematischen Unterschiede abzubilden. Wenn man so will, kann man den kompletten Lernprozess von der ersten Begegnung mit einem Elefanten an als Folge von Überraschungen verstehen, nach denen die Norm angepasst wurde. Aber üblicherweise sprechen wir von Norm und Überraschung erst, wenn der Lernprozess schon weiter fortgeschritten ist, denn vorher werden „Überraschungen“ quasi erwartet. Insofern spricht man anfangs eher von Prototypen statt von Normen.

Wir besitzen Normen oder Prototypen für alle möglichen Kategorien oder Mengen: Tiere, Restaurantbesuche, Bäume, Vorstellungsgespräche, Autos, gute Taten, Freunde, die Kategorie „Freund“, Lehrer, Ärztinnen, angemessenes Verhalten usw… Wenn Sie sich fragen, wie „man“ sich in Situation XY verhält, dann wollen Sie vermeiden, andere zu überraschen, indem Sie gegen deren Norm verstoßen. Denn Sie wissen, dass die anderen Ihr unpassendes Verhalten als Lernanlass nehmen würden – in dem Fall würden sie aus Ihrem unpassenden Verhalten auf Sie schließen. Sie wären nun der Neue, die Querschlägerin, der Unangenehme oder die Außergewöhnliche.

Kurz: Lernen lässt sich in weiten Teilen als statistischer Prozess verstehen (und modellieren, vgl. Frith 2014), in dem anhand von Beobachtungen ein Durchschnitt und eine Varianz ermittelt werden, die zu einem Prototyp oder einer Norm von einer Menge zusammengefasst werden. Zum Prototyp gehört das, was allen Elementen der Menge gemeinsam ist, wobei dies ungefähr (mit einer gewissen Varianz) oder als hartes Kriterium (ohne Varianz) gegeben sein kann. Durchschnitt und Varianz sind dabei sehr allgemein aufzufassen: Unser Prototyp eines Elefanten enthält keine Zahlenwerte für den Durchschnitt und die Varianz, sondern eher einen durchschnittlichen visuellen Eindruck. Dieser lässt sich zwar teilweise verbalisieren und ungefähr quantifizieren, aber dabei handelt es sich um zusätzliche Denkoperationen, die an die Vorstellung des eigentlichen Prototyps anknüpfen. Ebenso können wir sagen, ob ein bestimmtes Verhalten normal, also durchschnittlich ist oder nicht, ohne dass wir dafür einen numerischen Durchschnittswert angeben können. Das Erstellen von Prototypen und die Beurteilung von Normalität ist eine Operation von System 1, wohingegen exakte Quantifizierungen eine Operation von System 2 sind.

Als Erklärung für dieses statistische Lernen stelle ich mir Folgendes vor: Unsere Vorstellungen werden durch Aktivitätsmuster in der Aktivität unserer Neuronen enkodiert. Diese Aktivität wird durch die Verknüpfungen der Neurone untereinander bestimmt, weil sich die Aktivität nur darüber ausbreiten kann. Die neuronalen Verknüpfungen in unserem assoziativen Netzwerk werden jedes Mal verstärkt, wenn sie benutzt werden. Wenn sie aber nicht benutzt werden, verfallen sie mit der Zeit (das bekannte Prinzip „Use it or loose it“). Wenn wir nun mehrmals hintereinander Elefanten sehen und für die gleichen Assoziationen mit dem Elefanten (Farbe, Größe, Form, …) auch die gleichen Verknüpfungen genutzt werden, dann werden diese Verknüpfungen verstärkt, während seltene Assoziationen wie bestimmte Narben nur lose verknüpft bleiben. Wenn wir nun an die Menge der Elefanten denken, dann werden nur die Neuronen, deren Verknüpfungen eine gewisse Stärke aufweisen, aktiviert. Und dadurch wird automatisch der Prototyp der Menge, in dem sich die durchschnittlichen, gemeinsamen Merkmale vereinen, erzeugt.

Lernen von Mathematik

Betrachten Sie die folgenden Rechnungen:

\(1 = 1\)

\(1 + 3 = 4\)

\(1 + 3 + 5 = 9\)

\(1 + 3 + 5 + 7 = 16\)

\(1 + 3 + 5 + 7 + 9 = 25\)

…

Wenn Sie sich ein wenig mit den Rechnungen beschäftigen, werden Sie bald einige Regelmäßigkeiten erkennen:

• Auf der linken Seite wird immer ein Summand mehr addiert; auf der rechten Seite steht immer nur eine Zahl (das Ergebnis).
• Alle Summanden auf der linken Seite sind aufeinander folgende ungerade Zahlen; als nächster Summand wird stets die nächste ungerade Zahl gewählt, wobei die bisherigen Summanden stehen bleiben.
• Die Zahlen auf der rechten Seite sind die aufeinander folgenden Quadratzahlen.
• Die Summe aufeinander folgender ungerader Zahlen, bei 1 beginnend, ergibt immer eine Quadratzahl.

Zudem überraschen Sie diese Regelmäßigkeiten wahrscheinlich. Es entspricht nicht Ihrer Norm von allgemeinen Rechnungen, dass sich darin so viele Regelmäßigkeiten wiederfinden. Das macht diese Menge von Rechnungen besonders und interessant.

„Regelmäßigkeit“ ist hier (und in den meisten anderen Fällen) ein anderer Ausdruck für „Gemeinsamkeit“ oder „Invariante“. Und genau das meint auch der Begriff „Struktur“: Eine Invariante (Unveränderliche) in einer Menge. Dass die Mathematik auch als Strukturwissenschaft bezeichnet wird, zeigt, dass es in großen Teilen der Mathematik darum geht, Strukturen zu erkennen, zu formulieren und zu nutzen.

Wir nutzen Strukturen zum Beispiel zur Definition von Objekten. Die Menge der Quadrate ist dadurch definiert, dass alle Elemente vier gleich lange Seiten haben, zwischen denen ein rechter Winkel besteht. Die Menge der quadratischen Gleichungen ist dadurch definiert, dass sie sich auf die Form \(a \cdot x^2 + b \cdot x + c = 0\) mit reellen Zahlen \(a, b, c\) bringen lassen, wobei \(a\) nicht gleich \(0\) sein darf. Wir formulieren Strukturen, indem wir unsere natürliche Sprache oder die algebraische Symbolsprache benutzen. Und meine Hypothese ist, dass wir Strukturen erkennen, indem wir die Mengen, über die wir reden, durch Prototypen repräsentieren. So wie wir erkennen, dass alle Elefanten einen Rüssel haben, erkennen wir auch, dass alle obigen Rechnungen etwas gemeinsam haben.

Wenn wir uns vergegenwärtigen, dass unsere Wahrnehmungen, Gefühle und Gedanken durch neuronale Aktivitätsmuster enkodiert werden, dann macht es wohl keinen prinzipiellen Unterschied, ob wir den Durchschnitt von Größen, Farbtönen, Verhaltensweisen oder mathematischen Objekten wie den obigen Rechnungen bilden. Und mathematische Strukturen zeichnen sich schließlich dadurch aus, dass sie invariant sind, also harte Kriterien bilden. Sie sind ein Durchschnitt ohne Varianz.

Anders als bei den Strecken und den Elefanten weiter oben im Artikel geht es hier aber nicht um einen visuellen, bildlichen Prototyp, der von System 1 erstellt werden kann. Die Verarbeitung formal-symbolischer Darstellungen erfordert die Unterstützung von System 2 und ich denke, dass das Erkennen mathematischer Strukturen dementsprechend als Wechselwirkung der beiden Denksysteme verstanden werden kann. System 2 ermöglicht ein Verständnis der Darstellung, was z. B. bedeuten kann, dass die Darstellung in eine andere Darstellung oder Vorstellung übersetzt wird oder mit geeigneten Beispielen verknüpft wird. Dadurch kann System 1 Vorschläge für einen Prototyp machen, die System 2 wiederum präzisiert und formal-symbolisch formuliert.

Die Rechnungen oben können uns ein paar Beispiele geben: Wenn Sie zunächst nur die Teilmenge der Additionen auf der linken Seite des Gleichheitszeichens betrachten, dann erkennen Sie sofort, dass stets ein Summand dazukommt. Diese Eigenschaft der numerischen Darstellungen drückt sich schon bildlich durch die Stufenform aus. Dann betrachten Sie die Summanden: Sie alle sind in Ihrem assoziativen Netzwerk mit dem Namen „ungerade Zahl“ verknüpft, sodass die mühelos zu verarbeitende sprachliche Darstellung Sie auch auf diese Struktur bringt. Die dahinter stehende mathematische Struktur, dass alle diese Zahlen beim Teilen durch 2 den Rest 1 lassen, springt Ihnen wahrscheinlich nicht sofort ins Auge, sondern erfordert eine aktive Suche in Ihrem Gedächtnis. Auf diese Weise dient der Begriff jedoch als mühelos zu verarbeitender Anker, der auf eine komplexere Struktur verweisen kann. Außerdem sehen Sie durch die entsprechende Wiederholung in den Zeilen, dass die Terme immer mit 1 beginnen, worauf die nächsten ungeraden Zahlen folgen. Diese Strukturen waren alle recht leicht zu erkennen. Gleichzeitig dient vielleicht ein leichter zu behaltender Prototyp der Art „Summe ungerader Zahlen“ zur internen Repräsentation der Terme.

Betrachten Sie als Nächstes die Menge der Zahlen auf der rechten Seite des Gleichheitszeichens. Wenn Sie diese Zahlen nicht bereits als Quadratzahlen kennen und hier wiederum der Begriff als Anker für die mathematische Struktur greift, dann werden Sie die Struktur der Zahlen nicht sofort erkennen. Dazu muss dann System 2 aktiviert werden und gezielt nach Gemeinsamkeiten suchen, was z. B. über eine Faktorzerlegung geschehen kann, die offenbart, dass sich \(4\) als \(2 \cdot 2\), \(9\) als \(3 \cdot 3\) und \(16\) als \(4 \cdot 4\) schreiben lässt. Hier kann wiederum System 1 ansetzen, denn es handelt sich bei den Zahlen stets um dieselben geometrischen Formen, die durch ein Sternchen voneinander getrennt werden. Wenn zudem noch erkannt wird, dass sich auch \(1\) als \(1 \cdot 1\) schreiben lässt, dann lässt sich diese geometrische Intuition von System 2 auch so formulieren, dass die Zahlen auf der rechten Seite jeweils das Produkt der aufeinander folgenden natürlichen Zahlen mit sich selbst sind (bei 1 beginnend). Als einfacher, assoziierter Prototyp dient vielleicht die Vorstellung „Quadratzahlen“.

Betrachten Sie nun die Menge der Gleichungen, also jede Zeile als Element. Wie Sie relativ schnell erkannt haben, steht auf der linken Seite immer eine Summe aufeinander folgender ungerader Zahlen (bei 1 beginnend) und auf der rechten Seite immer eine Quadratzahl und nun erkennen Sie durch das immer gleiche Zeichen „=“, dass beide gleich groß sind. Sie können die bisher erkannten Strukturen miteinander verknüpfen, was in diesem Fall auf der sprachlichen Darstellungsebene passiert ist. Die Verknüpfung der Informationen legt nahe, dass dazu System 2 erforderlich ist, aber es kann ebenfalls vermutet werden, dass es Unterstützung durch System 1 erfährt, indem es die von System 2 präzise ausformulierten Prototypen der beiden Teilmengen intern aufrecht erhält.

Indem Sie also verschiedene Teilmengen betrachten und diese durch Prototypen repräsentieren, stoßen Sie schließlich auf das Gemeinsame, die Struktur in den Teilmengen der Rechnungen und der gesamten Menge der Rechnungen. Es wird Ihnen leicht fallen, die nächsten Glieder in der Folge der Rechnungen zu formulieren, weil Sie die jeweilige Struktur der Teilmengen auf den beiden Seiten des Gleichheitszeichens erfasst haben. Und Sie werden davon ausgehen, dass auch für diese neuen Rechnungen die vorher erkannte Struktur gilt, denn bisher fügte sich jede Rechnung ohne Abweichung in Ihren Prototyp ein. Das wird auch als Abstraktion oder als induktiver Schluss beschrieben.

Vermutlich kommt Ihnen dieser induktive Schluss ziemlich überzeugend vor. Sie haben eine empirisch-statistische Evidenz von fünf Rechnungen, die diesen Schluss belegen und das ist schon gar nicht schlecht. Wenn Sie sich an den ersten Blogartikel erinnern, erinnern Sie sich vielleicht auch an die assoziative Kohärenz. Die oben aufgeführten Rechnungen weisen durch den gemeinsamen Prototyp ohne Abweichung eine starke assoziative Kohärenz auf. Um sicher zu gehen, werden Sie intuitiv noch ein paar weitere Rechnungen anstellen und wenn Sie bei 10 oder 15 Rechnungen angelangt sind, scheint Ihnen die Evidenz wahrscheinlich ausreichend, um von Ihrem Schluss auf die zugrundeliegende Struktur völlig überzeugt zu sein. Genauso gehen Sie schließlich im Alltag ständig vor, meist werden Sie sogar schon nach nur zwei bis drei Beispielen von Ihrem Schluss auf die Struktur überzeugt sein, und Sie sind sehr erfolgreich damit. Doch den Mathematikern reicht das nicht. Sie haben ein paar unangenehme Überraschungen erlebt, in denen die statistische Evidenz überwältigend war und der vermutete Zusammenhang doch nicht galt und das hat ihre Norm von „Beweis“ nachhaltig verändert. Mathematische Zusammenhänge müssen durch Argumente und deduktive Schlüsse bewiesen werden.

Das Erkennen von Strukturen und die Denksysteme

Ich habe bereits oben beschrieben, dass das Schätzen einer durchschnittlichen Länge eine Operation von System 1 ist, also schnell, mühelos und größtenteils unbewusst abläuft. Ebenso erkennen Sie auch die Symmetrie eines Quadrats, eines Kreises oder einer Parabel, wobei man vor diesem Hintergrund die Symmetrieachse bzw. den Symmetriepunkt als durchschnittliche Lage der gesamten Punktmenge auffassen kann. Wie schon im zweiten Blogartikel geschrieben, bekommen wir über ikonische (bildliche) Darstellungen einen guten Zugang zu den Strukturen, weil diese in bildlichen Darstellungen durch Längen und Winkel dargestellt werden, die System 1 verarbeiten kann.

Ich denke, dass auch die Darstellung \(1 \cdot 1\), \(2 \cdot 2\), \(3 \cdot 3\), \(4 \cdot 4\), … bereits einen starken geometrischen Eindruck erzeugt, der System 1 die Struktur \(a \cdot a\) bzw. \(a^2\) erkennen lässt. Anders ist es bei \(1\), \(4\), \(9\), \(16\), … oder \(1\), \(3\), \(5\), \(7\), \(9\), … – dass diese Zahlen eine gemeinsame Struktur haben, ist nicht an der Darstellung zu erkennen. Hier kann es sein, dass die Zahlen bekannt sind und daher alle die gleiche Assoziation hervorrufen („Quadratzahlen“ bzw. „ungerade Zahlen“), was wiederum eine Operation von System 1 ist. Falls dies jedoch nicht der Fall ist, bedürfen die Zahlen einer näheren Untersuchung und ggf. einer anderen Darstellung, bei der mehrere Informationen beachtet und miteinander verknüpft werden müssen, was die Aktivierung von System 2 erfordert. Das gilt auch für das Erkennen der Struktur in den obigen Rechnungen, dass die Summe aufeinander folgender ungerader Zahlen, beginnend bei 1, immer eine Quadratzahl ergibt. Und spätestens bei der präzisen Formulierung der Struktur ist die Aufmerksamkeitsfokussierung und geistige Anstrengung, die nur System 2 aufbringen kann, unbedingt notwendig. Dennoch denke ich, dass System 2 beim Erkennen von Strukturen insgesamt eine viel bessere Unterstützung von System 1 erfährt als z.B. beim Kopfrechnen.

Vielleicht habe ich die Fähigkeiten von System 1 in Bezug auf Zahlen auch etwas untertrieben. Wir besitzen durchaus eine Art „Zahlensinn“, der es uns erlaubt, Zahlen intern durch eine ungefähre Vielfachheit oder Magnitude zu repräsentieren und sie dadurch zu verarbeiten. Dieser Magnitude kann eine räumliche Vorstellung (in Form einer Länge) zugrunde liegen (vgl. Dehaene 2011). In diesem Kontext lässt sich diese interne Magnitude einer Zahl vielleicht als Prototyp aller Mengen verstehen, die die gleiche Anzahl haben (z.B. 3 Bäume, 3 Mäuse, 3 Elefanten, 3 Menschen, 3 Häuser, 3 Punkte, 3 Quadrate, …). Als Gemeinsamkeit so unterschiedlicher Mengen bleibt nur die Anzahl übrig. Abgesehen von dieser Spekulation lässt sich aber festhalten, dass die Repräsentation von Zahlen durch eine ungefähre Magnitude eine Operation von System 1 sein muss, weil diese schnell und mühelos erfolgt. Dies ermöglicht uns schnelle, grobe Schätzungen für Rechnungen und es wird die Strukturerkennung in den obigen Rechnungen erleichtern, aber für die präzise Verarbeitung von Zahlen und die präzise Formulierung von Strukturen ist System 2 zuständig.

Am Ende des ersten Blogartikels habe ich eine Geschichte erwähnt, in der der Mathematiker Poincaré von einer plötzlichen mathematischen Eingebung berichtet, und ich habe das als Beispiel dafür angeführt, dass die mathematischen Fähigkeiten unseres Systems 1 nicht unterschätzt werden sollten bzw. teilweise noch gar nicht bekannt sind. Bei Poincarés Eingebung ging es um die Identität zweier Gruppen von Transformationen und vielleicht machen die Ausführungen in diesem Kapitel schon etwas verständlicher, dass das Unbewusste diese Abstraktion leisten konnte, bei der es schließlich auch um zwei Mengen geht, die anscheinend den gleichen Prototypen haben. Das bleibt jedoch an dieser Stelle eine vage Spekulation.

Didaktische Erklärungen und Folgerungen

Mit dem dargestellten statistischen Lernprozess lassen sich jedoch eine ganze Reihe an didaktischen Phänomenen erklären oder didaktischen Folgerungen ziehen. Dazu gehören:

• Regelverständnis: Während eine „mathematische“ Regel absolut und immer gilt, sind bei einer „statistischen“ Regel durchaus Ausnahmen (Ereignisse, die relativ stark vom Durchschnitt abweichen) erlaubt. Letzteres entspricht unserem intuitiven Regelverständnis und es muss deutlich gemacht werden, dass Ausnahmen bei einer mathematischen Regel nicht erlaubt sind. Der bekannte Spruch „Ausnahmen bestätigen die Regel“ gilt hier nicht.

• Kognitiver Konflikt: Schüler bringen aus dem Alltag viele Konzepte mit, die aus wissenschaftlicher Sicht falsch oder zumindest unpassend sind. Ein bekanntes didaktisches Manöver besteht darin, die Erwartungen, die aus diesen Alltagskonzepten entstehen, gezielt zu verletzen, sodass ein „kognitiver Konflikt“ entsteht, weil das bisherige Wissen nicht trägt. Wie erwähnt, sind solche Vorhersagefehler starke Lernanlässe, weil wir immer danach streben, alle unsere Assoziationen von Vorstellungen kohärent zu gestalten. Zum Beispiel denken viele Schüler, dass Socken (Kleidung insgesamt) immer warm halten. Wenn man jedoch einen Eisblock in einen Socken packt und einen weiteren daneben legt und vergleicht, welcher der beiden schneller schmilzt, stellt man fest, dass der Socken nicht generell warm hält, sondern nur den Wärmeaustausch verringert und somit isoliert. Hier wurde die statistische Basis um eine Beobachtung erweitert, die zur Anpassung des zugrundeliegenden Konzepts führen kann, wenn dies geeignet angeleitet wird. Ansonsten kann dieses Phänomen auch als „Ausnahme“ abgetan werden.

• Übergeneralisierung: Bei manchen Regeln wird der Gültigkeitsbereich zu groß angenommen, weil über lange Zeit keine Negativbeispiele behandelt werden. So wird zum Beispiel bei allen möglichen Rechnungen eine überwältigende statistische Evidenz für die Gültigkeit des Distributivgesetzes oder „ähnlicher“ Gesetze (vgl. die proportionale Funktion unten) gesammelt. Das ist in so unterschiedlichen Beispielen wie

  \(2 \cdot ( 3 + 4 ) = 2 \cdot 3 + 2 \cdot 4\);

  \(2 \cdot ( 3 – 4 ) = 2 \cdot 3 – 2 \cdot 4\);

  \(\frac{1}{2} \cdot ( 3 + 4 ) = \frac{1}{2} \cdot 3 + \frac{1}{2} \cdot 4\);

  \(( 3 – 4 ) : 2 = 3 : 2 – 4 : 2\);

  \(( \frac{3}{2} + \frac{4}{5} ) \cdot \frac{2}{6} = \frac{3}{2} \cdot \frac{2}{6} + \frac{4}{5} \cdot \frac{2}{6}\);

  bei einer proportionalen Funktion \(f\): \(f(2+3)=f(2)+f(3);\)

  der Fall gewesen und da ist es kein Wunder, wenn ein Fehler wie das Linearisieren der Wurzelfunktion ( \(\sqrt{a+b} = \sqrt{a} + \sqrt{b}\) ) oder das falsche Auflösen einer binomischen Formel ( \((a+b)^2 = a^2 + b^2\) ) auftritt. Es ist auch einigermaßen schwierig, diesen Fehler zu vermeiden, weil dazu eine neue Kategorie aufgemacht werden muss, obwohl der Ausdruck doch so gut in die alte Kategorie zu passen scheint und die statistische Evidenz dort sehr groß ist, sodass diese Ausnahme – statistisch gesehen – nicht unbedingt der Regel widersprechen muss. Dazu kommt, dass die Rückmeldung zu diesem Fehler in der Regel nicht unmittelbar erfolgt, sondern erst verzögert beim Vergleichen der Aufgaben. Dies erschwert es, die Assoziation zwischen der falschen Regel und der Erkenntnis „das war ein Fehler“ zu knüpfen, weil dazu beide Vorstellungen zeitlich nah beieinander liegen müssen (vgl. den Abschnitt im ersten Blogartikel zum assoziativen Gedächtnis).
  Durch das Stellen entsprechender Aufgaben kann es auch zu unerwünschten, übergeneralisierten Lerneffekten kommen wie „Bei Matheaufgaben müssen immer alle Zahlenangaben im Aufgabentext genutzt werden“, „Das Ergebnis ist fast immer ganzzahlig“ oder „Matheaufgaben lassen sich immer eindeutig lösen“.

• Lernen abstrakter Regeln: Abstrakte Regeln werden offenbar aus Beispielen generiert und behalten einen prototypischen Charakter. Laut Büchter und Leuders (2014, S. 66) berichten selbst erfahrene Mathematiker, dass sie über abstrakte Regeln und Objekte eher über Prototypen verfügen als über deren abstrakte Formulierung.
  Das Verständnis abstrakter Regeln wird dementsprechend nicht dadurch erreicht, indem man die abstrakt formulierte Regel präsentiert (und dann üben lässt), sondern indem man sie aus Beispielen ableitet. Dazu können am besten zunächst typische Beispiele gewählt werden, die den Schluss auf die abstrakte Regel oder den abstrakten Begriff leicht erscheinen lassen. Danach müssen jedoch „Grenzfälle“ folgen, die nicht besonders typisch erscheinen, aber trotzdem in die gleiche Kategorie (Beispiel der Regel oder des Begriffs) gehören, um die Reichweite dieser Kategorie auszuschärfen. Dazu können auch Grenzfälle gehören, die gerade nicht mehr zu der zugrundeliegenden Kategorie gehören.

• Sicherheit von induktiven Schlüssen: Schüler müssen erst lernen, dass die empirische Evidenz für einen induktiven Schluss nicht ausreicht, um diesen allgemeingültig zu beweisen. Die geistige Anstrengung, die das deduktive Schließen von ihnen verlangt, erscheint zunächst unnötig oder übertrieben und insofern ist es schwer, die Schüler dazu zu motivieren, ihre Schlüsse deduktiv abzusichern. Zum Teil kann in der Schule auch im Gegensatz zur universitären Mathematik auf intuitiv (z.B. anhand einer Skizze) begründete Schlüsse zurück gegriffen werden, weil der Anspruch dort geringer ist. Aber mit Hilfe von Beispielen, bei denen die intuitive Begründung fehlschlägt, sollte auch klar gemacht werden, welchen Wert deduktive Schlussfolgerungen für die Mathematik besitzen. Der Grad der assoziativen Kohärenz, der einen starken Eindruck von der Überzeugungskraft eines Schlusses erzeugt, aber gleichzeitig nur auf den eigenen Assoziationen zu diesem Schluss beruht, ist kein verlässliches Maß für die Gültigkeit von Urteilen, Zusammenhängen und Schlüssen.

Es lassen sich sicherlich weitere Phänomene finden, die sich vor dem Hintergrund des statistischen Lernens besser verstehen lassen und wenn Ihnen dazu etwas einfällt, dann schreiben Sie das gerne in die Kommentarspalte.

Wie die Mathematik so weit kommen konnte

Die hier vorgestellte statistische Form des Lernens erlaubt uns das Erkennen von Strukturen nicht nur in unserer Umwelt bei der Kategorisierung von Tieren und Pflanzen oder von Verhaltensweisen, sondern auch in der Mathematik. Sie ist weitgehend eine Operation von System 1 und verfügt damit über riesige Kapazitäten bei der Informationsverarbeitung. Diese können besonders bei der bildlichen Repräsentation von Strukturen effektiv genutzt werden. Für die präzise Formulierung oder Darstellung von Strukturen ist jedoch in der Regel System 2 notwendig, was besonders für symbolische Darstellungen gilt. Ebenso ist es notwendig, um die induktiven Schlüsse deduktiv zu beweisen und sie dadurch abzusichern. So kommt man in der Mathematik nicht um die Beschränkung auf die Ressourcen von System 2 herum, aber die Unterstützung von System 1 ist doch um einiges größer als sie nach dem ersten Blogartikel vielleicht erschien.

Quellen

Büchter, Andreas und Timo Leuders (2014): Mathematikaufgaben selbst entwickeln. Lernen fördern – Leistung überprüfen. 14. Auflage. Cornelsen.

Dehaene, Stanislas (2011): The Number Sense. How the Mind creates Mathematics. Revised and Updated Edition. Oxford University Press.

Frith, Chris (2014): Wie unser Gehirn die Welt erschafft. Auflage: 2010. Taschenbuch 2014. Springer Spektrum.

Kahneman, Daniel (2015): Schnelles Denken, langsames Denken. 14. Auflage. Pantheon-Ausgabe.